Das Haus des funktionalen Denkens – Entwicklung und Erprobung eines Modells für die Planung und Analyse methodischer und didaktischer Konzepte zur Förderung funktionalen Denkens
Thilo Höfer (2008): Das Haus des funktionalen Denkens – Entwicklung und Erprobung eines Modells für die Planung und Analyse methodischer und didaktischer Konzepte zur Förderung funktionalen Denkens. Dissertation, Pädagogische Hochschule Schwäbisch Gmünd.
Betreut durch Astrid Beckmann .
Begutachtet durch Astrid Beckmann und Claus Michelsen.
Tag der mündlichen Prüfung: 19.07.2008.
Zusammenfassung
Seit über 200 Jahren wird in der Mathematik der Begriff der Funktion verwendet. Das Verständnis für diesen Begriff hat sich in dieser Zeit ständig weiterentwickelt – und mit ihm die zugehörige Didaktik. Es entwickelten sich mehrere Modelle, die das Lernen von Funktionen, Funktionsbegriff und funktionalem Denken beschreiben und gleichzeitig die Möglichkeit enthalten, Probleme zu erfassen und Lösungsansätze zu entwickeln. Sie decken dabei prinzipiell zwei disjunkte Teilbereiche ab: Die Sichtweise (z. B. Sfard 1987 und Vollrath 1989) und die Darstellungsform (z. B. Swan 1982) von Funktionen. Aufgrund der Vielseitigkeit der auftretenden Problemfelder resultiert oft eine uneinheitliche didaktische Problemerfassung.
Die vorliegende Arbeit verfolgt das Ziel, die Lücke zwischen den beiden genannten Teilbereichen so zu überbrücken, dass ein gemeinsamer Rahmen entsteht. Innerhalb dieses Rahmens werden dann sowohl eine Eingliederung der vorhandenen Forschungsergebnisse, als auch die Konzeption und Analyse neuer Lösungsansätze ermöglicht. Als Kernstück der Arbeit wird dazu ein Modell, das Haus des funktionalen Denkens (Abb. 1), entwickelt und konkretisiert.
Die Erprobung des Modells erfolgte auf drei verschiedenen Forschungssträngen. So wurden zunächst die Vorkenntnisse im Bereich des funktionalen Denkens verschiedener Gruppen verglichen. Dazu wurden knapp 400 Schülerinnen und Schüler mit mittlerer Reife aus unterschiedlichen Schularten in einer quantitativen Studie auf ihre Fertigkeiten und Fähigkeiten im Bereich des funktionalen Denkens untersucht. Mit Hilfe des Modells wurden die Ergebnisse beschrieben, wobei ein Vergleich zwischen verschiedenen Schülergruppen möglich war (z. B. Realschüler und Gymnasiasten nach Klasse 10).
In einer zweiten Untersuchung wurden die Auswirkungen einer Unterrichtseinheit bezüglich der Kompetenzen im Bereich des funktionalen Denkens erfasst. Dabei wurde der durch eine Unterrichtseinheit entstandene Lernzuwachs qualitativ und quantitativ erfasst und im Haus des funktionalen Denkens eingeordnet. So können die durch die Unterrichtseinheit geförderten Kompetenzen innerhalb des Modells konkret eingeordnet werden. Diese Methode dient daher ganz allgemein dazu, Unterrichtssequenzen bezüglich des Haus des funktionalen Denkens zu kategorisieren. Eine Katalogisierung von Unterrichtssequenzen wird somit ermöglicht, aus der dann je nach Förderbedarf die entsprechende Sequenz ausgewählt werden kann.
Die dritte Untersuchung widmete sich dem Vergleich von Bildungsplänen bezüglich ihrer Kompetenzanforderungen. Die dazu durchgeführte Analyse verschiedener Bildungsstandards zeigt, wie die in ihnen enthaltenen Forderungen im Bereich des funktionalen Denkens mit Hilfe des Hauses des funktionalen Denkens kategorisiert und so direkt miteinander verglichen werden können.
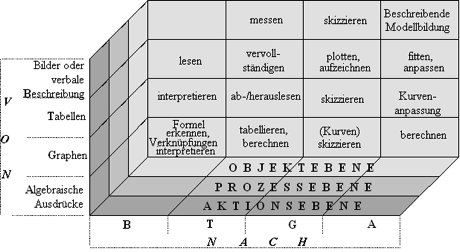
Abbildung 1: Das Haus des funktionalen Denkens
Sowohl diese konkreten Beispiele, als auch die anschließenden Ausblicke auf weitere Anwendungsmöglichkeiten zeigen, dass sich das Haus des funktionalen Denkens in vielfältigen und breit gefächerten Bereichen einsetzen lässt. Somit eignet es sich als Grundlage für Forschungen und Konzeptionen im Bereich des funktionalen Denkens.
Kontext
Literatur
- Sfard, A. (1987). Two Conceptions of Mathematical Notions: Operational and Structural. In: Proceedings of the 11th International Conference of PME, Vol. III, Montreal, S. 162-169
- Swan, M. (1982). The teaching of functions and graphs. In: Conference on functions, 1-5, S.151-165, Enschede
- Vollrath, H.-J. (1989). Funktionales Denken. In: Journal der Mathematikdidaktik 10, S.3-37