Baustelle:Unendliche Objekte
| Hinweise: |
Bitte beachten Sie die Madipedia:Richtlinien bei der Erstellung Ihres Beitrags. Insbesondere handelt es sich bei Enzyklopädie-Einträgen um Sekundärliteratur mit entsprechenden Hinweisen auf Primärliteratur. Bitte entfernen Sie diesen Hinweis und die jeweiligen Erläuterungstexte zu den Überschriften nachdem Sie den Artikel geschrieben haben.
| Hinweise: |
Wir empfehlen, den Artikel zunächst als Baustelle anzulegen, damit er noch nicht mit der Suchfunktion gefunden werden kann. So haben Sie die Möglichkeit, ihren Artikel in Ruhe auf einen guten Standard zu bringen. Einen Artikel zum Begriff "Funktion" würden Sie unter "Baustelle:Funktion" anlegen. Wenn der Artikel fertig ist, dann können Sie ihn in den normalen Bereich verschieben. Weitere Informationen dazu finden Sie unter Hilfe:Enzyklopädie.
In der projektiven Geometrie werden homogene Koordinaten genutzt, um die euklidische Ebene ohne Nullpunkt in den 3 zu integrieren. Hierbei spielen insbesondere die unendlichen Objekte Fernpunkte und Ferngeraden eine große Rolle. [1]
Fernpunkte
Fernpunkte sind Vektoren der Form T, die nicht mit Punkten der euklidischen Ebene identifizierbar sind. Um dennoch eine Interpretation herleiten zu können, werden Äquivalenzklassen betrachtet.
Herleitung
Sei Fehler beim Parsen (Syntaxfehler): {\displaystyle P(t)=(x·t,y·t,1)}
T ein Vektor, der mittels der Dehomogenisierung 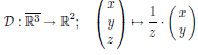 dem Punkt Fehler beim Parsen (Syntaxfehler): {\displaystyle (x·t,y·t)}
T der euklidischen Ebene zugeordnet werden kann. Da in der projektiven Geometrie skalare Vielfache miteinander identifiziert werden können, gilt Fehler beim Parsen (Syntaxfehler): {\displaystyle [P(t)]=[(x·t,y·t,1)}
TT]. Der Grenzwert Fehler beim Parsen (Syntaxfehler): {\displaystyle t→∞}
entspricht hierbei - anschaulich gesprochen - folgender Situation: Der Punkt bewegt sich auf einer Geraden, deren Richtung durch x und y festgelegt ist, in der Ebene immer weiter vom Ursprung weg.
dem Punkt Fehler beim Parsen (Syntaxfehler): {\displaystyle (x·t,y·t)}
T der euklidischen Ebene zugeordnet werden kann. Da in der projektiven Geometrie skalare Vielfache miteinander identifiziert werden können, gilt Fehler beim Parsen (Syntaxfehler): {\displaystyle [P(t)]=[(x·t,y·t,1)}
TT]. Der Grenzwert Fehler beim Parsen (Syntaxfehler): {\displaystyle t→∞}
entspricht hierbei - anschaulich gesprochen - folgender Situation: Der Punkt bewegt sich auf einer Geraden, deren Richtung durch x und y festgelegt ist, in der Ebene immer weiter vom Ursprung weg.
In Darstellung der homogenen Koordinaten gilt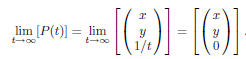 . Also repräsentieren alle Vektor der Form T unendlich weit entfernte Punkte, die sogenannten Fernpunkte. Diese können mit Richtungen von Geraden der euklidischen Ebene identifiziert werden, wobei andersherum für jede Geradenrichtung einen Fernpunkt existiert.
. Also repräsentieren alle Vektor der Form T unendlich weit entfernte Punkte, die sogenannten Fernpunkte. Diese können mit Richtungen von Geraden der euklidischen Ebene identifiziert werden, wobei andersherum für jede Geradenrichtung einen Fernpunkt existiert.
Ferngeraden
Alle Fernpunkte T liegen auf einer gemeinsamen Geraden: der Ferngeraden ∞T.
Erklärung
Auf jeder Geraden T mit Fehler beim Parsen (Syntaxfehler): {\displaystyle (a,b)≠(0,0)} liegt ein Fernpunkt T, denn es gilt für und . Dieser Fernpunkt T ist sogar der einzige Fernpunkt auf der Geraden g. Für die Ferngerade ∞T gilt für jeden Fernpunkt l∞, also liegen alle Fernpunkte auf der Ferngeraden ∞.
- ↑ Orendt, Thorsten; Richter-Gebert, Jürgen (2009): Geometriekalküle. Berlin, Heidelberg: Springer. Seite 2-6.













