Funktionsmaschine: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
| [unmarkierte Version] | [unmarkierte Version] |
| Zeile 1: | Zeile 1: | ||
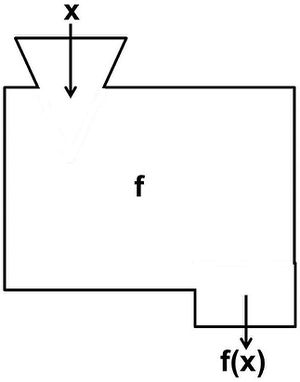
Das Prinzip einer Funktion kann mit dem Modell der Funktionsmaschine veranschaulicht werden. Auf anschauliche Art und Weise wird das Grundprinzip einer Input-Output-Maschine dargestellt: Die eingegebene Zahl (Input) wird durch die Maschine in genau definierter Funktion (Funktionsterm) bearbeitet und als veränderte Zahl wieder ausgegeben (Output). | Das Prinzip einer Funktion kann mit dem Modell der Funktionsmaschine veranschaulicht werden. Auf anschauliche Art und Weise wird das Grundprinzip einer Input-Output-Maschine dargestellt: Die eingegebene Zahl (Input) wird durch die Maschine in genau definierter Funktion (Funktionsterm) bearbeitet und als veränderte Zahl wieder ausgegeben (Output). | ||
| + | |||
| + | <br/> | ||
:'''[[Baustelle:Darstellungsarten von Funktionen|weitere Darstellungsarten von Funktionen]]''' | :'''[[Baustelle:Darstellungsarten von Funktionen|weitere Darstellungsarten von Funktionen]]''' | ||
| + | |||
| + | ==Beschreibung:== | ||
| + | [[Datei:Funktionsmaschine-groß.jpg| thumb |Beispiel einer Funktionsmaschine]] | ||
| + | Text | ||
| + | |||
| + | Text | ||
| + | |||
| + | Text | ||
| + | |||
| + | Text | ||
| + | |||
| + | Text | ||
==Exemplarische Beispielaufgaben aus der Schulbuchliteratur:== | ==Exemplarische Beispielaufgaben aus der Schulbuchliteratur:== | ||
Version vom 15. Januar 2013, 15:39 Uhr
Das Prinzip einer Funktion kann mit dem Modell der Funktionsmaschine veranschaulicht werden. Auf anschauliche Art und Weise wird das Grundprinzip einer Input-Output-Maschine dargestellt: Die eingegebene Zahl (Input) wird durch die Maschine in genau definierter Funktion (Funktionsterm) bearbeitet und als veränderte Zahl wieder ausgegeben (Output).
Beschreibung:
Text
Text
Text
Text
Text
Exemplarische Beispielaufgaben aus der Schulbuchliteratur:
- Gymnasium
- Klassenstufe 7:
- LS Lambacher Schweizer (2007): Mathematik Klasse 7, Klett, ISBN-10:3127345763, S.21