Funktion: mengentheoretische Auffassung: Unterschied zwischen den Versionen
| [gesichtete Version] | [gesichtete Version] |
K |
K |
||
| Zeile 10: | Zeile 10: | ||
| „'''Funktion'''“ ist eine Kurzbezeichnung für „rechtseindeutige Relation“. || | | „'''Funktion'''“ ist eine Kurzbezeichnung für „rechtseindeutige Relation“. || | ||
• „'''Abbildung'''“ ist meist ein Synonym für „Funktion“<br /> | • „'''Abbildung'''“ ist meist ein Synonym für „Funktion“<br /> | ||
| − | • „'''Operator'''“ und „'''Funktional'''“ bezeichnen jeweils | + | • „'''[[#Operator als Funktion|Operator]]'''“ und „'''[[#Operator als Funktion|Funktional]]'''“ bezeichnen jeweils Funktionen in speziellen Kontexten. |
|} | |} | ||
Die Schreib- bzw. Sprechweisen „<math>f</math> ''ist eine Funktion''“ und „<math>f</math> ''ist eine rechtseindeutige Relation''“ sind also gemäß dieser Definition gleichbedeutend. Ihr liegt Folgendes zugrunde: | Die Schreib- bzw. Sprechweisen „<math>f</math> ''ist eine Funktion''“ und „<math>f</math> ''ist eine rechtseindeutige Relation''“ sind also gemäß dieser Definition gleichbedeutend. Ihr liegt Folgendes zugrunde: | ||
| Zeile 76: | Zeile 76: | ||
| <div id="Funktionsgraph"></div><math>{{\operatorname{G}}_{f}}:=\{(x,f(x))|x\in A\}</math> || <math>{{\operatorname{G}}_{f}}</math> heißt '''Graph''' von <math>f</math> (oder einfach '''Funktionsgraph'''). Es gilt <math>{{\operatorname{G}}_{f}}\subseteq A\times B</math>. | | <div id="Funktionsgraph"></div><math>{{\operatorname{G}}_{f}}:=\{(x,f(x))|x\in A\}</math> || <math>{{\operatorname{G}}_{f}}</math> heißt '''Graph''' von <math>f</math> (oder einfach '''Funktionsgraph'''). Es gilt <math>{{\operatorname{G}}_{f}}\subseteq A\times B</math>. | ||
|} | |} | ||
| − | • Ein „'''Operator'''“ ist ebenfalls eine Funktion, in der höheren Mathematik meist von einem Vektorraum in einen Vektorraum, im Mathematikunterricht z. B. beim Aspekt „Bruch als Operator“.<br /> | + | <div id="Operator als Funktion"></div>• Ein „'''Operator'''“ ist ebenfalls eine Funktion, in der höheren Mathematik meist von einem Vektorraum in einen Vektorraum, im Mathematikunterricht z. B. beim Aspekt „Bruch als Operator“.<br /> |
• Ein „'''Funktional'''“ ist ein Operator von einem „Funktionenraum“ in <math>\mathbb{R}</math> oder <math>\mathbb{C}</math> (z. B. „bestimmtes Integral“). <ref>Das macht die frühere Bezeichnung „Funktionenfunktion“ für „Funktional“ plausibel..</ref> | • Ein „'''Funktional'''“ ist ein Operator von einem „Funktionenraum“ in <math>\mathbb{R}</math> oder <math>\mathbb{C}</math> (z. B. „bestimmtes Integral“). <ref>Das macht die frühere Bezeichnung „Funktionenfunktion“ für „Funktional“ plausibel..</ref> | ||
==Didaktische Vertiefung== | ==Didaktische Vertiefung== | ||
Version vom 21. August 2013, 06:39 Uhr
Verfasst von Horst Hischer
Übersicht
Die Untersuchung der kulturhistorischen Entstehung und Entwicklung des Funktionsbegriffs zeigt, wie sich aus ersten Ansätzen bei babylonischen Tabellen, bei der Erfindung von Notentexten, bei der Untersuchung und Darstellung zeitabhängigen Größen, bei freihändig gezeichneten „Kurven“, bei „analytischen Ausdrücken“ (als Termen) und bei graphischen und tabellarischen Darstellungen empirisch gewonnener Daten im 19. Jh. ein „termfreier“ Funktionsbegriff als „eindeutige Zuordnung“ entwickelt hat, der schließlich Anfang des 20. Jhs. auf der Grundlage der zuvor durch Georg Cantor begründeten Mengenlehre unter Bezug auf „geordnete Paare“ seine formal strenge und saubere Fassung als spezielle Relation erhalten hat. [1]
Grundlegende Definitionen
Unter Bezug auf den mit „binäre Relation“ bezeichneten Begriff lässt sich „Funktion“ knapp und elegant definieren, wobei hier statt „binäre Relation“ kurz „Relation“ gesagt wird: [2]
| Definition | Anmerkungen |
|---|---|
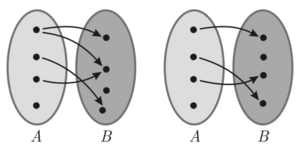
| „Funktion“ ist eine Kurzbezeichnung für „rechtseindeutige Relation“. |
• „Abbildung“ ist meist ein Synonym für „Funktion“ |
Die Schreib- bzw. Sprechweisen „Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} ist eine Funktion“ und „Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} ist eine rechtseindeutige Relation“ sind also gemäß dieser Definition gleichbedeutend. Ihr liegt Folgendes zugrunde:
| vorausgehende Definitionen | Erläuterungen |
|---|---|
| Voraussetzung: Es sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R} eine (binäre) Relation, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R\ne \varnothing} . Dann gilt: | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R}
ist also eine Menge von geordneten Paaren, z. B. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R\subseteq A\times B}
mit der nicht leeren „Ausgangsmenge“ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} und der nicht leeren „Zielmenge“ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle B} . (Man kann ggf. auch „leere Relationen“ und damit auch „leere Funktionen“ betrachten.) |
(1) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R}
ist genau dann rechtseindeutig, wenn für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x,{{y}_{1}},{{y}_{2}}}
gilt:
|
Jedem Element aus der Ausgangsmenge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A}
wird höchstens ein Element aus der Zielmenge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle B}
zugeordnet. Oder: Die Zuordnung verläuft von links nach rechts eindeutig. |
(2) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R}
ist genau dann linkseindeutig, wenn für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{x}_{1}},{{x}_{2}},y}
gilt:
|
Jedes Element aus der Zielmenge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A}
ist höchstens einem Element aus der Ausgangsmenge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle B}
zugeordnet. Oder: Die inverse Zuordnung verläuft von rechts nach links eindeutig. |
| (3) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R} ist genau dann injektiv, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle R} sowohl rechtseindeutig als auch linkseindeutig ist. | Die Zuordnung verläuft in beiden Richtungen eindeutig. Gleichbedeutend mit „injektiv“ ist „eineindeutig“. |
Weitergehende Definitionen und Bezeichnungen
| übliche Bezeichnungen bzw. symbolische Darstellungen | Erläuterungen |
|---|---|
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} sei eine (nicht leere) Funktion und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f\subseteq A\times B} mit nicht leeren Mengen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle B} . | (generelle Voraussetzung für das Folgende) |
| Es sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x\in A} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y\in B} . Falls von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} ein (und damit genau ein) Zuordnungspfeil nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y} verläuft, dann wird notiert:: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x\mapsto y} | gelesen: „dem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x}
wird das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y}
zugeordnet“ oder: „das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y}
wird dem Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x}
zugeordnet“ |
| Es sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x\in A} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y\in B} . Falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x\mapsto y} bezüglich der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} gilt, dann ist:: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x):=y} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)}
heißt dann Funktionswert von „Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x}
bezüglich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f}
, gelesen: „f von x“. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} muss nicht als Term darstellbar sein. [3] |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{D}}_{f}}:=\{x\in A|} es gibt ein Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y\in B} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y=f(x)\}} | Definitionsmenge von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f}
, auch „Definitionsbereich“, es ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{D}}_{f}}\subseteq A}
. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} ist Argument von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f\ \ :\Leftrightarrow \ \ x\in {{\operatorname{D}}_{f}}} . |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{W}}_{f}}:=\{y\in B|} es gibt ein Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x\in A} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y=f(x)\}} | Wertemenge von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} , auch „Wertebereich“, es ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{W}}_{f}}=\{f(x)|x\in A\}\subseteq B} . |
| Falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{D}}_{f}}=A} , dann wird notiert:: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f\,:A\to B} | gelesen: „Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f}
ist eine Funktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A}
in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle B}
“. Die Zuordnungspfeile Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mapsto}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \to}
sind streng zu unterscheiden, denn z. B. gilt: |
| Falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f\,:A\to B} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{W}}_{f}}=B} , dann heißt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} surjektiv. | Man sagt dann: „Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} ist eine Funktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle B} “ |
| Falls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} surjektiv und injektiv ist, dann heißt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} bijektiv. | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} ist dann eine Bijektion. |
| Eine beliebige Bijektion einer Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} auf sich selber ist eine Transformation von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} . | Automorphismen (z. B. in Algebra und Geometrie) sind stets strukturerhaltende Transformattonen. |
| Eine beliebige Transformation einer endlichen Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} ist eine Permutation . | Umordnungen der Elemente einer endlichen Menge sind stets Permutationen. |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{G}}_{f}}:=\{(x,f(x))|x\in A\}} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{G}}_{f}}} heißt Graph von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} (oder einfach Funktionsgraph). Es gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{G}}_{f}}\subseteq A\times B} . |
• Ein „Operator“ ist ebenfalls eine Funktion, in der höheren Mathematik meist von einem Vektorraum in einen Vektorraum, im Mathematikunterricht z. B. beim Aspekt „Bruch als Operator“.
• Ein „Funktional“ ist ein Operator von einem „Funktionenraum“ in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mathbb{R}} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \mathbb{C}} (z. B. „bestimmtes Integral“). [4]
Didaktische Vertiefung
Funktionsdefinition
- Ein wesentlicher Aspekt beim Funktionsbegriff ist die eindeutige Zuordnung, die mit „rechtseindeutig“ erfasst werden kann, ohne schon Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{D}}_{f}}:=\{x\in A|} es gibt ein Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y\in B} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y=f(x)\}} mit voraussetzen zu müssen.
- Wenn die Ausgangsmenge mit dem Definitionsbereich übereinstimmt, wenn also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{D}}_{f}}:=\{x\in A|} es gibt ein Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y\in B} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y=f(x)\}} gilt, wird jedem Element der Ausgangsmenge genau ein Element der Zielmenge zugeordnet, so dass also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f\,:A\to B} gilt. Es bietet sich für den Mathematikunterricht an, mit dieser engeren Sichtweise zu beginnen (und ggf. dabei zu bleiben).
- Der Aspekt der eindeutigen Zuordnung liegt in zweispaltigen Tabellen automatisch vor, wenn sich in der „Eingangspalte“ (links) kein Element wiederholt. Damit kann eine „Funktion“ alternativ von Anbeginn an auch mit einer solchen Tabelle identifiziert werden, dieses in Übereinstimmung mit der Auffassung der Numeriker und ganz in der kulturhistorischen Tradition der Mathematik von den Babyloniern bis Du Bois-Reymond (s. o).
- Die symbolische Darstellung „Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f\,:A\to B} “ ist eine Aussage (bzw. Eigenschaft) und bedeutet definitionsgemäß und ist so zu lesen: „Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} ist eine Funktion von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle B} “. Damit ist es sprachlich nicht korrekt, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f\,:A\to B} eine „Funktion“ zu nennen, sondern korrekt wäre z. B. entweder „die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle B} “ oder „die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} mit der Eigenschaft Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f\,:A\to B} “.
- Es ist zu beachten, dass bei Funktionen der mit dem Symbol Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} bezeichnete „Funktionswert“ (ganz im Sinne der kulturhistorischen Tradition) nicht notwendig ein Term sein muss, so dass man hier besser nicht immer von einem „Funktionsterm“ sprechen sollte. Ganz anders ist die Situation bin Funktionenplottern, die nur die Darstellung termdefinierter Funktionen ermöglichen können.
- Offensichtlich kann man nicht termdefinierbare Funktionen mit endlichem Definitionsbereich durch eine Tabelle darstellen. Aber das ist auch bei nicht endlichem Definitionsbereich möglich, wie etwa folgendes Beispiel zeigt: Es sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(n)} für alle natürlichen Zahlen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle n} die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle n} -te Dezimalstelle von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \pi} , also Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(0)=3} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(1)=1} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(2)=4} ..., dann lässt sich dies mit einer (gedachten!) unendlichen Tabelle erfassen.
- Nur dann, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y=f(x)} gilt und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} für alle betrachteten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} ein Term ist, kann man also „Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle y=f(x)} “ eine Funktionsgleichung nennen.
Funktionsgraph
- Die übliche o. g. Definition des Funktionsgraphen gemäß Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{G}}_{f}}:=\{(x,f(x))|x\in A\}} resultiert aus dem Wunsch der Darstellung der Wertepaare Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (x,f(x))} durch Punkte in einem Koordinatensystem, wobei diese Wertepaare Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (x,f(x))} nicht notwendig numerischer Art sein müssen. Wenn nun aber eine Funktion formal streng als spezielle Relation definiert wird und eine Relation ja gerade eine Menge geordneter Paare ist, so erhalten wir Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f=\{(x,f(x))|x\in A\}={{\operatorname{G}}_{f}}} .
- Konsequenz: Es gibt in formaler Hinsicht keinen Unterschied zwischen „Funktion“ und „Funktionsgraph“, wenn man beide so wie oben mengentheoretisch definiert. Das hat zur weiteren Konsequenz, dass der „Funktionsgraph“ bereits eine Funktion ist und man in der Tat beispielsweise eine „Parabel als quadratische Funktion“ auffassen kann. [5] Auch der von einem Funktionenplotter erzeugte Funktionsplot kann damit als eine „Funktion“ aufgefasst werden. [6]
Diese Betrachtungen führen zunächst zu einer „Weite“ des mit „Funktion“ bezeichneten Begriffs auf und leiten ueber zu den vielen „Gesichtern von Funktionen“. [7] Zugleich ist anzumerken, dass die mengentheoretische Auffassung von „Funktion als rechtseindeutiger Relation“ beweistechnisch gute Möglichkeiten eröffnet und dass in diesem Zusammenhang in „sauberer“ Sprechweise möglichst unterschieden werden sollte zwischen „die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} “, „der Funktionswert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} “ und „graphische Darstellung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} “.
Literatur
- Deiser, Oliver [2010]: Einführung in die Mengenlehre. Berlin / Heidelberg: Springer (3., korrigierte Auflage; 1. Auflage 2000; 2., korrigierte und erheblich erweiterte Auflage 2004).
- Felgner, Ulrich [2002]: Der Begriff der Funktion. In: Felix Hausdorff – Gesammelte Werke Band II, Grundzüge der Mengenlehre. New York / Berlin / Heidelberg: Springer, S. 621–633.
- Herget, Wilfried & Malitte, Eva & Richter, Karin [2000]: Funktionen haben viele Gesichter – auch im Unterricht! In: Flade, Lothar & Herget, Wilfried (Hrsg.): Mathematik lehren und lernen nach TIMSS – Anregungen für die Sekundarschulen. Berlin: Verlag Volk und Wissen, 2000, 115–124.
- Hischer, Horst [2012]: Grundlegende Begriffe der Mathematik: Entstehung und Entwicklung. Struktur – Funktion – Zahl. Wiesbaden: Springer Spektrum.
Anmerkungen
- ↑ Vgl. hierzu die ausführlichen Betrachtungen in [Hischer 2012, Kapitel 4 und 5].
- ↑ Auch [Deiser 2010] definiert „Funktion“ als rechtseindeutige Relation.
- ↑ Vgl. die Anmerkungen zur kulturhistorischen Genese des Funktionsbegriffs bezüglich Fourier und Dirichlet.
- ↑ Das macht die frühere Bezeichnung „Funktionenfunktion“ für „Funktional“ plausibel..
- ↑ Vgl. die in der Übersicht erwähnte kulturhistorische Entstehung und Entwicklung des Funktionsbegriffs.
- ↑ Genauer: Sowohl die erwähnte „Parabel“ als auch die Funktionsplots sind eigentlich „Darstellungen“ einer Funktion, was die Frage aufwirft, worin der Unterschied zwischen einer Darstellung und dem dadurch Dargestellten besteht.
- ↑ Vgl. [Herget et. al. 2020].
| Der Beitrag kann wie folgt zitiert werden: Madipedia (2013): Funktion: mengentheoretische Auffassung. Version vom 21.08.2013. In: madipedia. URL: http://madipedia.de/index.php?title=Funktion:_mengentheoretische_Auffassung&oldid=12242. |