Funktionsgraph

Schaubild einer abstrakten diskreten Funktion

Schaubild einer konkreten diskreten Funktion: Zeitabhängigkeit der Temperaturentwicklung

Schaubild einer kontinuierlichen Funktion: Modellfunktion zum Zeit-Weg-Gesetz einer gleichmäßig beschleunigten Bewegung

Übersicht

• Streng genommen ist zwischen „Funktionsgraph“ (als Menge geordneter Paare) und der visualisierenden Darstellung durch ein „Schaubild“ zu unterscheiden:
  

Definition:

Es sei $f$ eine Funktion von der Argumentmenge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} in die Zielmenge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle B} , kurz: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f\,:A\to B} .

Dann ist der Funktionsgraph von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} durch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{G}}_{f}}:=\{(x,f(x))|x\in A\}} definiert.

Der Funktionsgraph einer (einstelligen) Funktion [math]f[/math] von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle B} besteht also aus allen geordneten Paaren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (x,f(x))} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x\in A} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)\in B} .
(Dabei ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle A} die Definitionsmenge von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} , die kurz mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{D}}_{f}}} bezeichnet wird. Die Einschränkung auf einstellige Funktionen ist nicht notwendig, wenngleich sie aber in den meisten unterrichtsrelevanten Fällen üblich ist.)

Visualisierung von Funktionsgraphen

• Funktionsgraphen lassen sich z. B. in einem kartesischen Koordinatensystem visualisieren, indem die geordneten Paare Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle (x,f(x))} durch „Punkte“ mit der Abszisse Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle x} (nach rechts auf der Rechtsachse bzw. der 1. Koordinatenachse) und der Ordinate Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f(x)} (nach oben auf der Hochachse bzw. der 2. Koordinatenachse) abgetragen werden. Insbesondere Funktionsgraphen reeller Funktionen werden auf diese Weise visualisiert.
• Anstelle eines kartesischen Koordinatensystems sind auch andere zweidimensionale Koordinatensysteme möglich, z. B. Polarkoordinatensysteme. Und auch dreidimensionale Koordinatensysteme (z. B. für kartesische Koordinaten, Zylinderkoordinaten, Kugelkoordinaten) können einer Visualisierung dienen, so etwa von Raumkurven oder Flächen.)
• Solche Visualisierungen können insbesondere zeichnerisch (von Hand als Skizze oder mit Hilfe von Zeicheninstrumenten) oder mit Hilfe von Funktionenplottern erfolgen. Die dabei erzeugten Zeichnungen oder Funktionsplots sind aber nur Darstellungen eines gegebenen Funktionsgraphen und nicht mit diesem identisch. Jede solche visualisierende Darstellung ist ein Schaubild des Funktionsgraphen und also solche nur eine Simulation des Graphen bzw. der Funktion. Solche Schaubilder sind ikonische Repräsentationen einer Funktion.
• Ein (formaler) Funktionsgraph wird also durch ein (konkretes) Schaubild visualisiert und ist von diesem zu unterscheiden.
• Einem konkreten Funktionsgraphen kann man verschiedene Schaubilder zuordnen.
• Legt man die mengentheoretische Identität einer Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f} gemäß Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle f=\{(x,f(x))|x\in A\}} zugrunde, so folgt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle {{\operatorname{G}}_{f}}=f} .

Beispiele

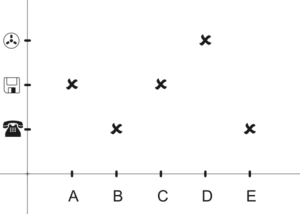
• Das erste Beispiel zeigt ein Schaubild einer nicht-numerischen diskreten Funktion, bei der jedem abstrakten Objekt A, B, C, ... eindeutig ein symbolisch dargestelltes technisches Objekt zugeordnet wird.
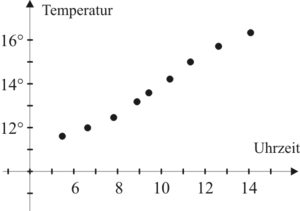
• Das zweite Beispiel zeigt ein Schaubild einer diskreten numerischen Funktion, bei der einigen Tageszeitpunkten eindeutig eine bestimmte Temperatur zugeordnet wird.
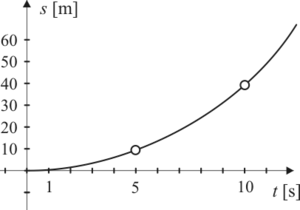
• Das dritte Beispiel zeigt ein Schaubild einer kontinuierlichen Modellfunktion des Zeit-Weg-Gesetzes einer gleichmäßig beschleunigten Bewegung. Erkennbar wird hier, dass nach der doppelten Zeitdauer der vierfache Weg zurückgelegt wird.

Literatur

• Hischer, Horst [2016]: Mathematik – Medien – Bildung. Medialitätsbewusstsein als Bildungsziel: Theorie und Beispiele. Wiesbaden: Springer Spektrum.

Der Beitrag kann wie folgt zitiert werden: Madipedia (2016): Funktionsgraph. Version vom 15.06.2016. In: madipedia. URL: http://madipedia.de/index.php?title=Funktionsgraph&oldid=24747.