Weg-Zeit-Diagramme: Unterschied zwischen den Versionen
| [gesichtete Version] | [gesichtete Version] |
K |
|||
| Zeile 1: | Zeile 1: | ||
Weg-Zeit-Diagramme sind eine spezielle Form der Darstellung von Sachverhalten, bei denen der Weg ''s'' von der Zeit ''t'' abhängt. | Weg-Zeit-Diagramme sind eine spezielle Form der Darstellung von Sachverhalten, bei denen der Weg ''s'' von der Zeit ''t'' abhängt. | ||
| − | Dabei wird die Zeit ''t'' auf der | + | Dabei wird die Zeit ''t'' auf der Abszissenachse, der Weg ''s'' auf der Ordinatenachse abgetragen. |
| − | Die Durchschnittsgeschwindigkeit kann mit Hilfe des Differenzenquotienten <math>\frac{\Delta s}{\Delta t}</math> ermittelt werden. Die Geschwindigkeit zu einem bestimmten Zeitpunkt entspricht dem Differentialquotienten <math>\lim\limits_{\Delta t \rightarrow 0}{\frac{\Delta s}{\Delta t}}</math> | + | Die Durchschnittsgeschwindigkeit kann mit Hilfe des Differenzenquotienten <math>\frac{\Delta s}{\Delta t}</math> ermittelt werden. Die Geschwindigkeit zu einem bestimmten Zeitpunkt entspricht dem Differentialquotienten <math>\lim\limits_{\Delta t \rightarrow 0}{\frac{\Delta s}{\Delta t}}</math>, der ersten Ableitung an der Stelle <math>t_0</math>. |
== Anwendung im Mathematikunterricht == | == Anwendung im Mathematikunterricht == | ||
| − | Für den Mathematikunterricht kann man diese Form der Darstellung von Funktionen nutzen, um die Begriffe Ableitung, Differenzenquotient, Anstieg | + | Für den Mathematikunterricht kann man diese Form der Darstellung von Funktionen nutzen, um die Begriffe Ableitung, Differenzenquotient, Anstieg usw. praxisnah zu erklären. Dabei kann eine Verbindung zum Physik-Unterricht und umgekehrt hergestellt werden. |
== Beispielaufgaben == | == Beispielaufgaben == | ||
| Zeile 32: | Zeile 32: | ||
|} | |} | ||
| − | Zeichnet man diese Werte in ein Weg-Zeit-Diagramm, so entsteht folgender Graph: | + | Zeichnet man diese Werte in ein Weg-Zeit-Diagramm und vervollständigt sie geeignet, so entsteht folgender Graph: |
[[Datei:Auto1.jpg|600px]] | [[Datei:Auto1.jpg|600px]] | ||
| − | <math> s(t)</math> ist eine [[Lineare Funktionen|lineare Funktion]]. Der Anstieg der Funktion entspricht der Durchschnittsgeschwindigkeit und kann über das Steigungsdreieck (Differenzenquotient) ermittelt werden: | + | <math> t \rightarrow s(t)</math> ist eine [[Lineare Funktionen|lineare Funktion]]. Der Anstieg der Funktion entspricht der Durchschnittsgeschwindigkeit und kann über das Steigungsdreieck (Differenzenquotient) ermittelt werden: |
| − | <math>m={\frac{\Delta s}{\Delta t}}={\frac{ | + | <math>m={\frac{\Delta s}{\Delta t}}={\frac{20 m-5 m}{4 s-1 s}}=5 \frac{m}{s}=\overline v</math>. |
Damit hat man für die Bewegung des Autos eine Funktion gefunden: | Damit hat man für die Bewegung des Autos eine Funktion gefunden: | ||
| − | <math>s(t)=5\frac{m}{s} \cdot t</math> | + | <math>t \rightarrow s(t)=5\frac{m}{s} \cdot t</math> |
| − | Die Momentangeschwindigkeit z.B. zum Zeitpunkt <math>t=2, | + | Die Momentangeschwindigkeit z. B. zum Zeitpunkt <math>t=2,5 s</math> ermittelt man durch Bilden der Ableitung der Funktion <math>s(t)=5 \frac{m}{s} \cdot t</math> und Einsetzen von <math>t=2,5 s</math>: |
<math>v(t)=s'(t)=5\frac{m}{s}</math> | <math>v(t)=s'(t)=5\frac{m}{s}</math> | ||
| − | + | Das Auto fährt, egal zu welchem Zeitpunkt, mit konstanter Geschwindigkeit. Es handelt sich um eine gleichförmige Bewegung. | |
| − | <math>v(t=2, | + | <math>v(t=2,5 s)=s'(t=2,5 s)=5 \frac{m}{s}</math> |
| − | === | + | === Gleichmäßig beschleunigte Bewegung === |
| − | Etwas eindrucksvoller ist die Betrachtung einer | + | Etwas eindrucksvoller ist die Betrachtung einer gleichmäßig beschleunigten Bewegung, etwa beim Anfahren eines Autos an einer Ampel: |
Eine Auto beschleunige mit <math>a=3\frac{m}{s^2}</math>. Folgende Messwerte wurden aufgenommen: | Eine Auto beschleunige mit <math>a=3\frac{m}{s^2}</math>. Folgende Messwerte wurden aufgenommen: | ||
| Zeile 89: | Zeile 89: | ||
Auch hier kann man die Durchschnittsgeschwindigkeit anhand des Differenzenquotienten ermitteln. | Auch hier kann man die Durchschnittsgeschwindigkeit anhand des Differenzenquotienten ermitteln. | ||
| − | Die Funktion <math>s(t)=\frac{a}{2}t^2+v_0t+s_0</math> beschreibt die Bewegung des Fahrzeugs. Da das Auto keine Anfangsgeschwindigkeit <math>v_0</math> hat und der Anfangsweg <math>s_0</math> ebenfalls 0 ist, verschwinden diese Terme | + | Die Funktion <math>t \rightarrow s(t)=\frac{a}{2}t^2+v_0t+s_0</math> beschreibt die Bewegung des Fahrzeugs. Da das Auto hier keine Anfangsgeschwindigkeit <math>v_0</math> hat und der Anfangsweg <math>s_0</math> ebenfalls 0 ist, verschwinden hier diese Terme in dieser Gleichung. |
| − | Es interessiert die (Momentan-) Geschwindigkeit zum Zeitpunkt <math>t=3, | + | Es interessiert die (Momentan-)Geschwindigkeit zum Zeitpunkt <math>t=3,5 s</math>. |
<math>v(t)=s'(t)=2\cdot \frac{a}{2} \cdot t=a \cdot t</math> | <math>v(t)=s'(t)=2\cdot \frac{a}{2} \cdot t=a \cdot t</math> | ||
| − | <math>v(t=3, | + | <math>v(t=3,5 s)=s'(t=3,5 s)=3\frac{m}{s^2} \cdot 3,5 s=10,5 \frac{m}{s} </math> |
Interessant wird die Aufgabe nun, wenn man die Problematik der Gefahrenbremsung betrachtet: | Interessant wird die Aufgabe nun, wenn man die Problematik der Gefahrenbremsung betrachtet: | ||
| − | Das Auto kann mit einer maximalen negativen Beschleunigung <math>a</math> bremsen/verzögern. Nun kommt ein Hindernis vor das Auto, welches mit einer bestimmten | + | Das Auto kann mit einer maximalen negativen Beschleunigung <math>a</math> bremsen/verzögern. Nun kommt ein Hindernis vor das Auto, welches mit einer bestimmten (Anfangs-)Geschwindigkeit <math>v_0</math> fährt. Unter Berücksichtigung einer Reaktionszeit ist zu berechnen, ob es das Auto schafft, rechtzeitig zum Stillstand zu kommen. |
Sollte dies nicht der Fall sein, so kann man die Geschwindigkeit beim Aufprall bestimmen. | Sollte dies nicht der Fall sein, so kann man die Geschwindigkeit beim Aufprall bestimmen. | ||
Version vom 13. November 2015, 12:11 Uhr
Weg-Zeit-Diagramme sind eine spezielle Form der Darstellung von Sachverhalten, bei denen der Weg s von der Zeit t abhängt.
Dabei wird die Zeit t auf der Abszissenachse, der Weg s auf der Ordinatenachse abgetragen.
Die Durchschnittsgeschwindigkeit kann mit Hilfe des Differenzenquotienten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \frac{\Delta s}{\Delta t}} ermittelt werden. Die Geschwindigkeit zu einem bestimmten Zeitpunkt entspricht dem Differentialquotienten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle \lim\limits_{\Delta t \rightarrow 0}{\frac{\Delta s}{\Delta t}}} , der ersten Ableitung an der Stelle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t_0} .
Anwendung im Mathematikunterricht
Für den Mathematikunterricht kann man diese Form der Darstellung von Funktionen nutzen, um die Begriffe Ableitung, Differenzenquotient, Anstieg usw. praxisnah zu erklären. Dabei kann eine Verbindung zum Physik-Unterricht und umgekehrt hergestellt werden.
Beispielaufgaben
Gleichförmige Bewegung
Ein Auto fahre mit konstanter Geschwindigkeit von A nach B. Dabei hat es folgende Wege nach folgenden Zeiten zurückgelegt:
| Weg in m | Zeit in s |
|---|---|
| 5 | 1 |
| 10 | 2 |
| 15 | 3 |
| 20 | 4 |
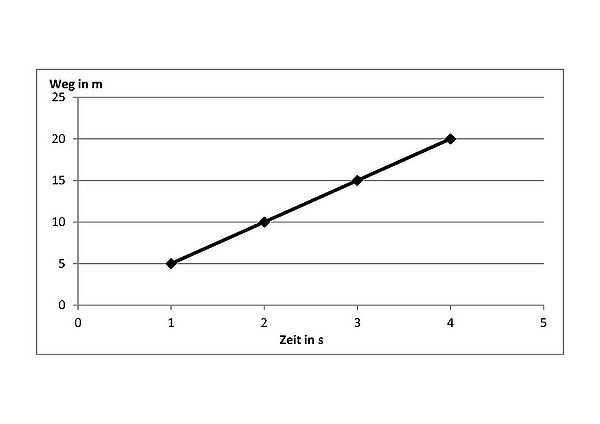
Zeichnet man diese Werte in ein Weg-Zeit-Diagramm und vervollständigt sie geeignet, so entsteht folgender Graph:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t \rightarrow s(t)} ist eine lineare Funktion. Der Anstieg der Funktion entspricht der Durchschnittsgeschwindigkeit und kann über das Steigungsdreieck (Differenzenquotient) ermittelt werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle m={\frac{\Delta s}{\Delta t}}={\frac{20 m-5 m}{4 s-1 s}}=5 \frac{m}{s}=\overline v} .
Damit hat man für die Bewegung des Autos eine Funktion gefunden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t \rightarrow s(t)=5\frac{m}{s} \cdot t}
Die Momentangeschwindigkeit z. B. zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t=2,5 s} ermittelt man durch Bilden der Ableitung der Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle s(t)=5 \frac{m}{s} \cdot t} und Einsetzen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t=2,5 s} :
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v(t)=s'(t)=5\frac{m}{s}}
Das Auto fährt, egal zu welchem Zeitpunkt, mit konstanter Geschwindigkeit. Es handelt sich um eine gleichförmige Bewegung.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v(t=2,5 s)=s'(t=2,5 s)=5 \frac{m}{s}}
Gleichmäßig beschleunigte Bewegung
Etwas eindrucksvoller ist die Betrachtung einer gleichmäßig beschleunigten Bewegung, etwa beim Anfahren eines Autos an einer Ampel:
Eine Auto beschleunige mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a=3\frac{m}{s^2}} . Folgende Messwerte wurden aufgenommen:
| Weg in m | Zeit in s |
|---|---|
| 1,5 | 1 |
| 6 | 2 |
| 13,5 | 3 |
| 24 | 4 |
| 37,5 | 5 |
| 54 | 6 |
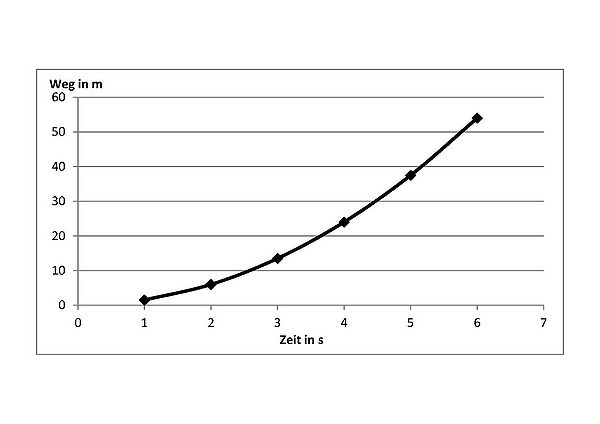
Hier erhält man für das Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle s(t)} -Diagramm folgenden Graph:
Der entstandene Funktionsgraph ist ein Teil einer Parabel 2. Grades.
Auch hier kann man die Durchschnittsgeschwindigkeit anhand des Differenzenquotienten ermitteln.
Die Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t \rightarrow s(t)=\frac{a}{2}t^2+v_0t+s_0} beschreibt die Bewegung des Fahrzeugs. Da das Auto hier keine Anfangsgeschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v_0} hat und der Anfangsweg Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle s_0} ebenfalls 0 ist, verschwinden hier diese Terme in dieser Gleichung.
Es interessiert die (Momentan-)Geschwindigkeit zum Zeitpunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle t=3,5 s} .
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v(t)=s'(t)=2\cdot \frac{a}{2} \cdot t=a \cdot t}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v(t=3,5 s)=s'(t=3,5 s)=3\frac{m}{s^2} \cdot 3,5 s=10,5 \frac{m}{s} }
Interessant wird die Aufgabe nun, wenn man die Problematik der Gefahrenbremsung betrachtet:
Das Auto kann mit einer maximalen negativen Beschleunigung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a} bremsen/verzögern. Nun kommt ein Hindernis vor das Auto, welches mit einer bestimmten (Anfangs-)Geschwindigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v_0} fährt. Unter Berücksichtigung einer Reaktionszeit ist zu berechnen, ob es das Auto schafft, rechtzeitig zum Stillstand zu kommen. Sollte dies nicht der Fall sein, so kann man die Geschwindigkeit beim Aufprall bestimmen.
| Der Beitrag kann wie folgt zitiert werden: Madipedia (2015): Weg-Zeit-Diagramme. Version vom 13.11.2015. In: madipedia. URL: http://madipedia.de/index.php?title=Weg-Zeit-Diagramme&oldid=22784. |